Rejection sampling
In mathematics, rejection sampling is a basic pseudo-random number sampling technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm".
It generates sampling values from an arbitrary probability distribution function  by using an instrumental distribution
by using an instrumental distribution 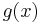 , under the only restriction that
, under the only restriction that 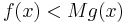 where
where 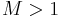 is an appropriate bound on
is an appropriate bound on 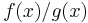 .
.
Rejection sampling is usually used in cases where the form of  makes sampling difficult. Instead of sampling directly from the distribution
makes sampling difficult. Instead of sampling directly from the distribution  , we use an envelope distribution
, we use an envelope distribution 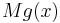 where sampling is easier. These samples from
where sampling is easier. These samples from 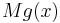 are probabilistically accepted or rejected.
are probabilistically accepted or rejected.
This method relates to the general field of Monte Carlo techniques, including Markov chain Monte Carlo algorithms that also use a proxy distribution to achieve simulation from the target distribution  . It forms the basis for algorithms such as the Metropolis algorithm.
. It forms the basis for algorithms such as the Metropolis algorithm.
The unconditional acceptance probability is the proportion of proposed samples which are accepted, which is 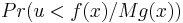
![= E[f(x)/Mg(x)] =](/2012-wikipedia_en_all_nopic_01_2012/I/b49c9d2890905d52e0e8b7498ade5e02.png) ∫
∫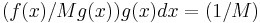 ∫
∫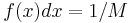 . If
. If  is low, fewer samples are rejected, and the required number of samples for the target distribution is obtained more quickly. Because
is low, fewer samples are rejected, and the required number of samples for the target distribution is obtained more quickly. Because  must be no less than the maximum of
must be no less than the maximum of 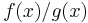 , the unconditional acceptance probability is higher the less that ratio varies, however to obtain acceptance probability 1,
, the unconditional acceptance probability is higher the less that ratio varies, however to obtain acceptance probability 1,  , which defeats the purpose of sampling.
, which defeats the purpose of sampling.
Contents |
Algorithm
The algorithm (used by John von Neumann and dating back to Buffon and his needle) is as follows:
- Sample
 from
from 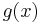 and
and  from
from 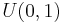 (the uniform distribution over the unit interval)
(the uniform distribution over the unit interval) - Check whether or not
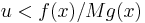 .
.
- If this holds, accept
 as a realization of
as a realization of  ;
; - if not, reject the value of
 and repeat the sampling step.
and repeat the sampling step.
- If this holds, accept
The validation of this method is the envelope principle: when simulating the pair 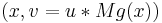 , one produces a uniform simulation over the subgraph of
, one produces a uniform simulation over the subgraph of 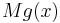 . Accepting only pairs such that
. Accepting only pairs such that 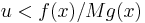 then produces pairs
then produces pairs 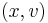 uniformly distributed over the subgraph of
uniformly distributed over the subgraph of  and thus, marginally, a simulation from
and thus, marginally, a simulation from  .
.
This means that, with enough replicates, the algorithm generates a sample from the desired distribution  . There are a number of extensions to this algorithm, such as the Metropolis algorithm.
. There are a number of extensions to this algorithm, such as the Metropolis algorithm.
Examples
As a simple geometric example, suppose it is desired to generate a random point within the unit circle. Generate a candidate point 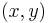 where
where  and
and  are independent uniformly distributed between −1 and 1. If it so happens that
are independent uniformly distributed between −1 and 1. If it so happens that 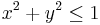 then the point is within the unit circle and should be accepted. If not then this point should be rejected and another candidate should be generated.
then the point is within the unit circle and should be accepted. If not then this point should be rejected and another candidate should be generated.
The ziggurat algorithm, a more advanced example, is used to efficiently generate normally-distributed pseudorandom numbers.
Drawbacks
Rejection sampling can lead to a lot of unwanted samples being taken if the function being sampled is highly concentrated in a certain region, for example a function that has a spike at some location. Also, as the dimensions of the problem get larger, the ratio of the embedded volume to the "corners" of the embedding volume tends towards zero, thus a lot of rejections can take place before a useful sample is generated, thus making the algorithm inefficient and impractical. See curse of dimensionality.
See also
References
- Robert, C.P. and Casella, G. "Monte Carlo Statistical Methods" (second edition). New York: Springer-Verlag, 2004.
- J. von Neumann, "Various techniques used in connection with random digits. Monte Carlo methods", Nat. Bureau Standards, 12 (1951), pp. 36–38.